Wrong precedence
Archives Forums/BlitzMax Bug Reports/Wrong precedence
| ||
| The precedence (a.k.a order of operations) is something we all learned and we are all very well used to. That's why we make use of it whenever it allows us to save some brackets. But beware! BlitzMax seems to mess up something here. Example: Mathematically, these to terms are exactly the same: -1*(-10)^2 -(-10)^2 We have (in both cases): ten, negative, which we square, which again we then have to multiply by minus one. The multiplication by -1 is (in both cases) the last operation that must be executed - also by, but not limited to, the definition found on wikipedia. So, without further calculations, it is possible to say that the result will be negative, since the preceding squaring turns pretty much everything into positive numbers. Now look how BlitzMax follows those rules: Print (-1*(-10)^2) +" "+ (-(-10)^2) As you can see, the negation, when using -(-10), is applied before squaring, which (to get to the point), just cost me some f***ing nerves. Seriously, I think this should be fixed. Mathematics is *very* often used in programming, so it would be really nice if you could at least rely on standards there. Greetings and so |
| ||
| They Should give different results (-(-10)) is a unary operation NOT a subtraction and a multiplication. I was going to provide a link to this , BUT imagine my surprise that the page you posted to support your statement is exactly the same one I was going to post against it. So please read your own link. notably the bit helpfully titled "Programming languages" Last edited 2011 |
| ||
| In that Wikipedia article the Programming Languages section makes it clear that there really is no standard, as does the Gaps in the Standard section. The BlitzMax precedence table is not part of the online manual so I can't link to it. It is in the Expressions section of the Language Reference. Here is a "link": (YourBlitzMaxFolder)/docs/html/Language/Expressions/index.html As someone with a mathematical education I think the BlitzMax precedence is wrong in some cases and -x^2 should evaluate as -(x^2). It also gives And the same precedence as Or, when And should have higher precedence. So these are all wrong, meaning they differ from what I expect. But BlitzMax is behaving correctly in that it follows its own documented rules. It was released in 2005 and the precedence table is not going to change now. By the way, it also associates exponentiation incorrectly, evaluating a^b^c as (a^b)^c rather than a^(b^c). |
| ||
| @Floyd So -10^2 should be -100? Well I agree with you, shame the OP is talking about (-(-10)^2). (I agree in that written down I would expect that. Meaning when I see -10 superscript 2 I think of -(10^2), but when I see -10^2 I think of (-10)^2. Possible because my maths background is engineering?) Hes talking about the unity operators in general, whereas you are talking about a specific common problem of expressing -ten squared as opposed to minus(10 squared). Both his examples are -ten squared, he is saying that -1*(-x)^2 is the same as -(-x)^2 and is only using squared to show it isn't by sign Many programming languages use precedence levels that conform to the order commonly used in mathematics, though some, such as APL and Smalltalk, have no operator precedence rules (in APL evaluation is strictly right to left, in Smalltalk it's strictly left to right). I would say this isn't saying there is no standard, but that some languages don't use itThe logical bitwise operators in C (and all programming languages that borrowed precedence rules from C, for example, C++, Perl and PHP) have a precedence level that the creator of the C language considers to be unsatisfactory.[4] However, many programmers have become accustomed to this order. The relative precedence levels of operators found in many C-style languages are as follows: Last edited 2011 |
| ||
| Ah, thanks. I didn't think about the unary operator. Well, i somehow did, but I expected the unary operator only to apply to numerals, not to expressions like (-10). But yeah, of course, the BlitzMax documentation makes it clear and I see that BMax is following it's rules (which, I guess, it inherited from C). By the way: Despite your mathematical education; in our school, the solution to -10^2 was considered to be -100. Always. No exceptions. Valid for all schools and courses I visited - but surprisingly some math teachers told us that there exist universities, where '-10' is considered as a value and therefore -10^2 results in 100. I never believed that. But by looking at your "mathematical education" statements I begin to believe for once, what those teachers told me. Maybe you are both mathematical educated, but simply not within the meaning of the same standard. Sounds plausible. =edit= shame on you, H&K. My last paragraph doesn't make sense anymore since you edited your post =( Last edited 2011 |
| ||
| lol the last edit was 14Mins before your post ;) |
| ||
My reading of this bug report was that something is wrong with the precedence of unary minus. But the example obscured the real problem.Print (-1*(-10)^2) +" "+ (-(-10)^2)This compares -1*x^2 with -x^2 where x has the value -10. BlitzMax precedence, highest to lowest, is unary minus then exponentiation then multiplication. -1*x^2 is evaluated as (-1)*(x^2) which is -1 * 100 = -100 -x^2 is evaluated as (-x) ^ 2 which is (--10) ^ 2 = 100 If the relative precedence of unary minus and exponentiation is reversed they both yield -100, as I would expect. This is the problem mentioned in the Gaps in the Standard part of the article. The C/C++ style table in the Programming Languages section is not enlightening because they use a function call for exponentiation rather than an operator. |
| ||
| If the relative precedence of unary minus and exponentiation is reversed they both yield -100, as I would expect. But as Holz pointed out he was told at school that some Universities treat -10^2 the way you dont, so at the very least Bodmas sufferers from the same lack of standard that computer languages do.The thing is we have both probably been programming long enough to know to bracket when in doubt. Re. A^B^C Lol, unless we are working on rings rather than fields that's a very academic correction ;) |
| ||
Honestly, I first thought this "bug" - or let's call it behavior - was new, because I never realized that sort of operation doing not what I expected before. And I use gaussian functions very often. (Yeah, that's what I did, i tried to implement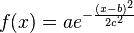 I went through most of my old codes to see what I did then. And the terms were always of the form dx=c*(x-b) y=a*Exp(-dx*dx) I guess that explains a lot... ;) |
| ||
| Re. A^B^C Lol, unless we are working on rings rather than fields that's a very academic correction ;) This post snippet by me is totally wrong I can see what he posted, but cut and pasted it thinking it said something else. Pardons to anyone whose time machine failed due to this. |
   |